P3372 【模板】线段树 2 DRAFT

¹

题目描述

如题，已知一个数列，你需要进行下面三种操作：

• 将某区间每一个数乘上 $x$
• 将某区间每一个数加上 $x$
• 求出某区间每一个数的和

输入格式

第一行包含三个整数 n,m,p，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含 n 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 m 行每行包含若干个整数，表示一个操作，具体如下：

操作 $1$： 格式：1 x y k 含义：将区间 $[x,y]$ 内每个数乘上 $k$

操作 $2$： 格式：2 x y k 含义：将区间 $[x,y]$ 内每个数加上 $k$

操作 $3$： 格式：3 x y 含义：输出区间 $[x,y]$ 内每个数的和对 $p$ 取模所得的结果

输出格式

输出包含若干行整数，即为所有操作 $3$ 的结果。

输入输出样例

输入 #1

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出 #1

17
2

说明/提示

【数据范围】

对于 $30\%$ 的数据：$n \le 8$，$m \le 10$ 对于 $70\%$ 的数据：$n \le 10^3$，$m \le 10^4$ 对于 $100\%$ 的数据：$n \le 10^5$，$m \le 10^5$

除样例外，$p = 571373$

（数据已经过加强^_^）

样例说明：

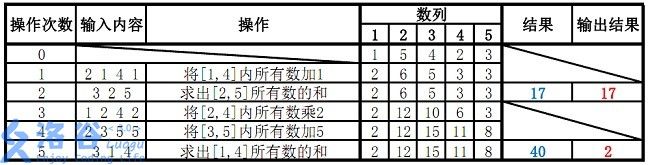
故输出应为 $17$、$22(40 \bmod 38 = 2)$

所以

真的有那么亿点点难理解，也还不怎么会，学的时候主要是看 线段树 - OI Wiki 的代码 和 题解 P3373 【【模板】线段树 2】 - lqhsr 的博客 的思路

一个讲的挺明白的，一个代码看着挺明白的 :trophy:

结构体函数

之前学结构体的时候知道里面可以定义函数，也只是知道，从来没用过。 这题因为经常要 mod，配合结构体函数还是挺方便的。

struct Test {
    int test1, test2, test3;
    void mod() {
        test1 %= p;
        test2 %= p;
        test3 %= p;
    }
}test[100];

test[k].mod();

懒标记下传

和线段树 1 比，多了一个乘法，所以多了乘法懒标记，初值为 1。 乘法懒标记下传时需要对 加法懒标记、乘法懒标记和值 进行乘法。 区间乘法也同样的需要对这三个值进行乘法。 其他的基本和线段树 1 一样。

懒标记下传的代码确实挺长的，但理清思路发现还是比较好理解的。

1. 乘法懒标记不为 1，则需要下传。 分左右儿子，每边先把所有的乘法做好，再 .mod() 最后父亲乘法懒标记赋值为 1
2. 加法懒标记不为 0，则需要下传。也分左右儿子 儿子懒标记加上父亲懒标记 儿子值加上 （父亲懒标记 * 儿子所办含的节点数） 再 .mod() 最后父亲懒标记归零

区间修改

整体思路和线段树 1 的一样，乘法的区间修改唯一的区别就在最后一步

if (l<=s && t<=r) {
    tree[k].m *= c;
    tree[k].f *= c;
    tree[k].w *= c;
    tree[k].mod();
    return;
}

完整代码

#include <cstdio>

long long n, m, d, x, y, at, c, p;
struct node {
    long long l, r, w, f, m;
    void mod() {
        w %= p;
        f %= p;
        m %= p;
    }
}tree[400010];

long long read() {
    bool flag = false; long long x = 0; char ch = getchar();
    while(ch<'0' || ch>'9') {if(ch == '-') flag = 1; ch = getchar();}
    while(ch>='0' && ch <= '9') {x *= 10; x += ch - '0'; ch = getchar();}
    return flag ? - x : x;
}

void build(long long l, long long r, long long k) {
    long long mid = (l + r) / 2;
    tree[k].l = l, tree[k].r = r, tree[k].m = 1;
    if (l == r) {
        tree[k].w = read();
        return;
    }
    build(l, mid, 2*k);
    build(mid+1, r, 2*k+1);
    tree[k].w = tree[2*k].w + tree[2*k+1].w;
    tree[k].mod();
}

void down(long long k) {
    long long lson = 2 * k, rson = 2 * k + 1;
    int m = tree[k].m, f = tree[k].f;
    if (tree[k].m != 1) {
        tree[lson].w *= m;
        tree[lson].f *= m;
        tree[lson].m *= m;
        tree[lson].mod();

        tree[rson].w *= m;
        tree[rson].f *= m;
        tree[rson].m *= m;
        tree[rson].mod();

        tree[k].m = 1;
    }
    if (f) {
        tree[lson].f += f;
        tree[lson].w += f * (tree[lson].r - tree[lson].l + 1);
        tree[lson].mod();

        tree[rson].f += f;
        tree[rson].w += f * (tree[rson].r - tree[rson].l + 1);
        tree[rson].mod();

        tree[k].f = 0;
    }
}

void cheng(long long l, long long r, long long k, long long c) {
    long long s = tree[k].l, t = tree[k].r;
    long long mid = (s + t) / 2;

    if (l<=s && t<=r) {
        tree[k].m *= c;
        tree[k].f *= c;
        tree[k].w *= c;
        tree[k].mod();
        return;
    }

    down(k);
    if (l <= mid) cheng(l, r, 2*k, c);
    if (r >= mid + 1) cheng(l, r, 2*k+1, c);

    tree[k].w = tree[2*k].w + tree[2*k+1].w;
    tree[k].w %= p;
}

void add(long long l, long long r, long long k, long long at) {
    long long s = tree[k].l, t = tree[k].r;
    long long mid = (s + t) / 2;

    if (l<=s && t<=r) {
        tree[k].f += at;
        tree[k].w += at * (t - s + 1);
        tree[k].mod();
        return;
    }

    down(k);
    if (l <= mid) add(l, r, 2*k, at);
    if (r >= mid + 1) add(l, r, 2*k+1, at);

    tree[k].w = tree[2*k].w + tree[2*k+1].w;
    tree[k].mod();
}

long long get(long long l, long long r, long long k) {
    long long s = tree[k].l, t = tree[k].r, sum = 0;
    long long mid = (s + t) / 2;

    if (l<=s && t<=r) {
        return tree[k].w;
    }

    down(k);
    if (l <= mid) sum += get(l, r, 2*k);
    sum %= p;
    if (r >= mid + 1) sum += get(l, r, 2*k+1);
    return sum % p;
}

int main() {
    n = read(), m = read(), p = read();
    build(1, n, 1);

    while (m--) {
        d = read(), x = read(), y = read();
        if (d == 1) {
            c = read();
            cheng(x, y, 1, c);
        }
        else if (d == 2) {
            at = read();
            add(x, y, 1, at);
        }
        else printf("%lld\n", get(x, y, 1));
    }
    return 0;
}